”5人が一列に並ぶとき、全部で何通りの並び方がありますか?”
一つ一つの場合を調べなくとも、計算一つで求められることも多いのが、この「場合の数」。
式を立てるとパッと答えが出るのですが、その計算式、人に説明できますか?
場合の数(並べ方)の計算について、仕組みを理解しましょう!
問題1 AからCまで行くのに何通り?

先生、”場合の数”って、いちいち調べなきゃいけなくて大変です。パッと求められる方法はないですか?

はい、調べなきゃいけない大変な問題もあるけれど、問題によっては計算式一つで求められるものもあるね。
今日は、計算で求められる”場合の数”を3題練習してみよう!

樹形図で解く

まずは4年生で学習した内容の復習で、”樹形図”を使って解いてみよう!

はい、わかりました。”樹形図”をかいてみます。
まず、それぞれの道に記号を付けました。
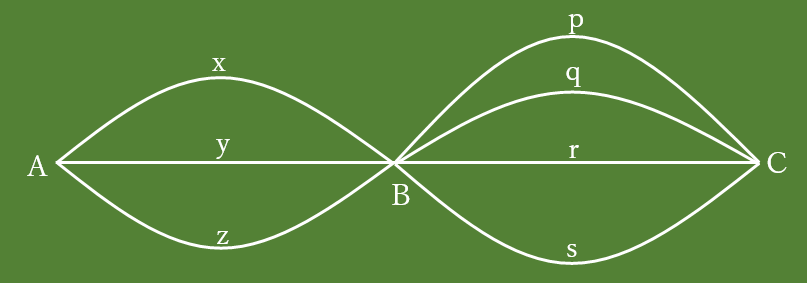

AからBまでの道に”x”を選んだときの樹形図をかきます。
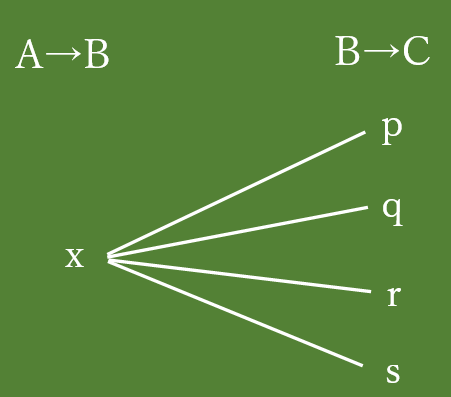

AからBまでの道に”x”を選んだとき、BからCまでの道には、”p”で行くか、”q”で行くか、”r”で行くか、”s”で行くか、で4通りあります。

素晴らしい!ここまでバッチリだね!

AからBまでの道に”y”を選んだときと、”z”を選んだときは、”x”のときと同じだから、それぞれ4通りずつあるので、もう樹形図はかく必要ないですよね。
ということで、4通り×3=12通りです。

完璧だ!”x”のときの樹形図だけかければ、他は必要ないね!それで、4通りの樹形図が3パターンできるから、4×3で求められた!
この樹形図が基本になっているんだけれど、パッと計算で求める方法をやってみよう!
計算でパッと解く

はい、サクッと計算で求められる方法を教えてください!

考え方の基本は樹形図なんだけれど、この黒板を見てみよう!
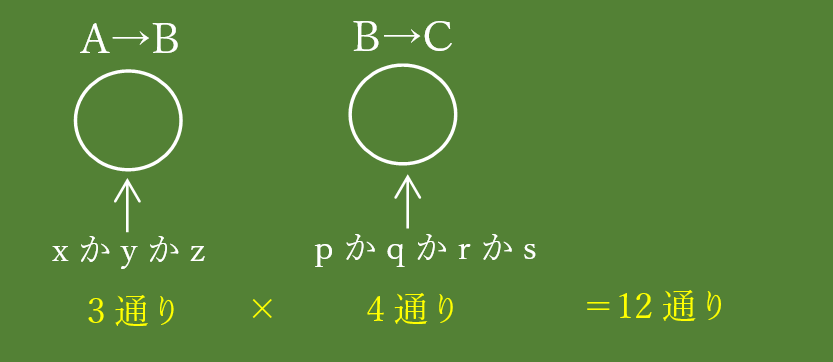

AからBまでは3通りの行き方があって、BからCまでは4通りの行き方があって、それをかけ算するだけ!
さっき樹形図をかいたので、この式で求められるっていうことが、なんかわかります!

それはよかった!
A→Bの3通りに対して、B→Cはそれぞれ4通りあるから、3×4となるんだけど、言葉だけで説明されてもなかなかしっくりいかない。太郎くんの言うように、樹形図で一度理解しておくと、この式も理解しやすくなるんだ。
問題1のような”かけ算の考え方”を、積の法則といいます。
問題2 5人の並び方は何通り?

じゃあ、2問目いってみよう!

(1)5人の並び方

早速、計算の方法を使ってみます!
左から順番に並べていくことにして、、、
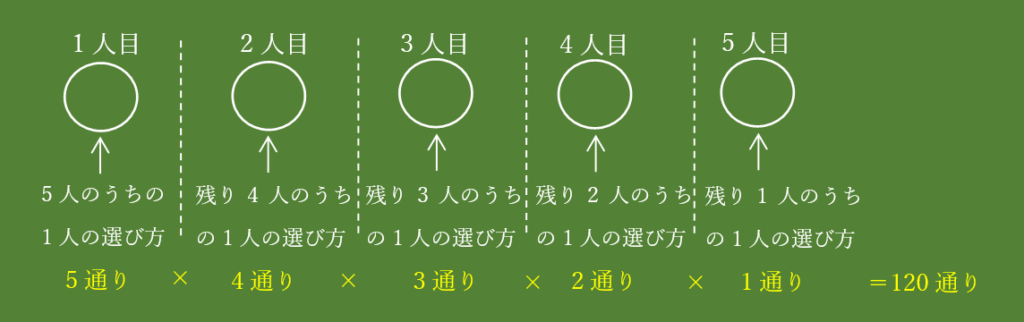

見事!
慣れてきたら、ノートには「5×4×3×2×1=120通り」だけでいいね!
じゃあ、(2)いってみよう!
(2)両端が父と母になる並び方

(2)は、両端が父と母のときの並べ方ですね。
両端は父と母だから、まず真ん中3人の並べ方を考えます。
左から順番に並べていくことにして、、、
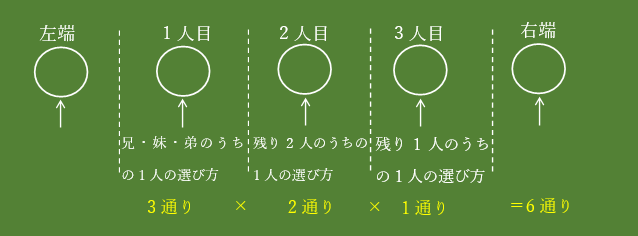

真ん中3人の並び方は6通りになりました。
答えは6通りでいいのかな・・・

あと一歩!真ん中3人の並び方は6通りで合ってるんだけど、両端について考えてあげよう!

あっ、左端に父がくる場合と、母がくる場合の2パターンあります!
だから、6通り×2=12通りになりました!

その通り!父と母の並び方が2通りあるってことだね!
それに対して、子どもの並び方が6通りで、6×2になるわけだ!


この問題では、両端の父と母の並び方2通りを忘れてしまうことが多いから、注意しよう!
問題3 3けたの整数のつくり方は何通り?

じゃあ、最後の問題、3問目いってみよう!

(1)整数は何通り?

さっきのように左から、つまり、百の位から順番に並べていきますね。

そう!この問題では、百の位がポイントだ!百の位にもってきてはいけないカードがあるから、気を付けよう!

百の位に”0”のカードは使えないので、そこは1、2,3のカードのどれかで3通りになりました。
十の位は、百の位に1枚カードを使うと、残りが3枚で3通り。
一の位は、百の位と十の位に1枚ずつカードを使うと、残りが2枚で2通りです。
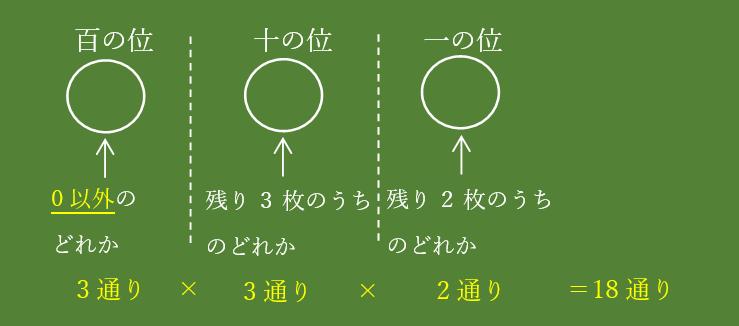

大正解!!完璧だ!!
”0”のカードがあるときは、百の位に気をつけなくちゃいけない。
十の位と一の位は何の数字がきてもいいから、まずは百の位から決めていくことがポイント!
(2)偶数は何通り?

最後はちょっと難しいぞ。
百の位に”0”は使ってはいけないという制約があるし、一の位にも気をつけなくちゃいけない!
○○2や、〇〇8、○○0のように、一の位が”0”か偶数であれば、その数は偶数になります。
偶数になるための条件は、一の位が”0”か偶数であるということ!

百の位と一の位に気をつけなくちゃいけないってことで、どっちから考えていけばいいのか・・・
百の位は、1,2,3の3通りで、一の位は0、2の2通りですよね?
一の位に”0”を使うときは、百の位は3通りあるけれど、一の位に2を使うときは、百の位は1か3で2通りになってしまいます。。。

そうなんだ!その通りなんだ!
太郎くんの言うように、一の位に”0”を使うか、”2”を使うかで、百の位に使えるカードが異なってくるから、”場合分け”が必要になるんだ!

一の位に”0”を使う場合と、”2”を使う場合で、分けて考えるってことですね!
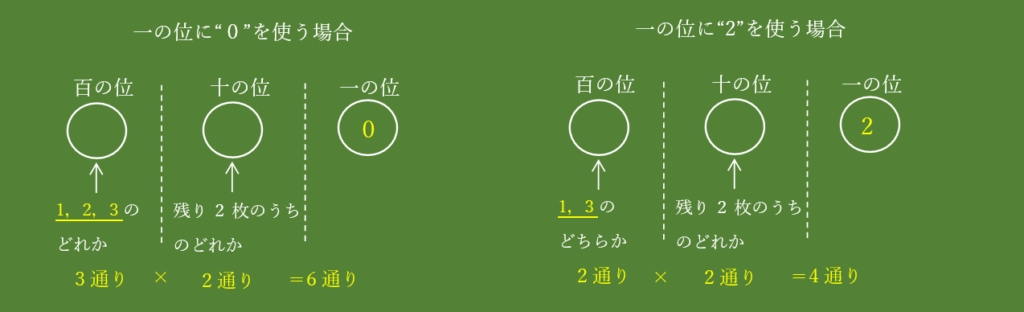

一の位で場合分けして、6通り+4通り=10通りになりました!

見事!大正解だ!
計算式一つでパッと求められるものもあれば、場合分けして、それぞれで計算式が必要なものもある。
一つステップアップするために、この場合分けはとても大切なんだ!
まとめ
並べ方の問題では、かけ算の式で何通りかを求められることがわかりました。
それでも慣れてくると、”なんでこの式になるんだろう?”、”これは足すのか、かけるのか、どっちなんだろう?”と疑問がわいてくることがあります。
そのときは、基本に立ち返って樹形図をかいてください!
樹形図をかくことで、計算式の意味が確認できます!


