”5人の中から2人の日直を選ぶとき、全部で何通りの並び方がありますか?”
一つ一つの場合を調べなくとも、計算一つで求められることも多いのが、この「場合の数」。
式を立てるとパッと答えが出るのですが、その計算式、人に説明できますか?
場合の数(組み合わせ)の計算について、仕組みを理解しましょう!
5人の中から2人を選ぶ計算

場合の数の”並べ方”の計算については、わかったんですけど、”組み合わせ”の計算がいまいちよくわかりません。
÷2をするとか、÷3でしたっけ?、÷6でしたっけ?どっちだか・・・

よくある質問だ。
じゃあ、一つ例題を通して”組み合わせ”の計算式の確認をしよう!


これ、最後に”÷2”をする問題だったと思うんですが、なんで÷2をするのかがわかりません・・

まずは、組み合わせを考える前に、5人の中から2人を取り出して”並べる”んだ。
並べ方は計算でパッと求められるけど、説明のために書き出しておこう!
左側は2人を並べる場合を書き出して、右側は計算して20通りと求めました。
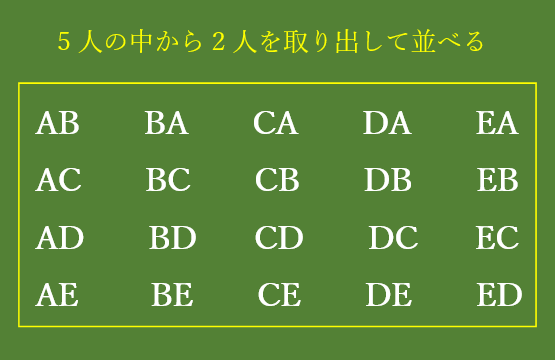
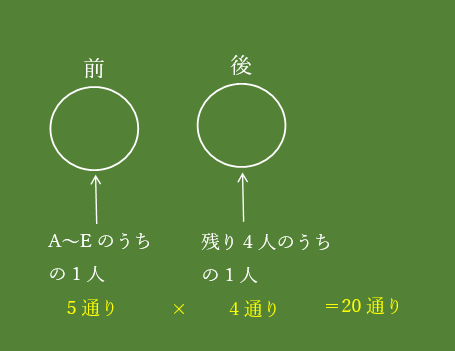

2人の”並べ方”だったら、5×4=20通りと求まりますね。
でも、日直2人を選ぶ”組み合わせ”ですよね。。。並べ方じゃなくて・・・

太郎くん、左の図をよく見てみよう!
並べ方だったら、確かにこの20通りなんだけれど、同じ組み合わせになるっていうのが無いかな?

あー、ABとBAが同じです!ACとCAも同じです!
並べ方だったら異なりますけど、組み合わせだったら同じになりますね!
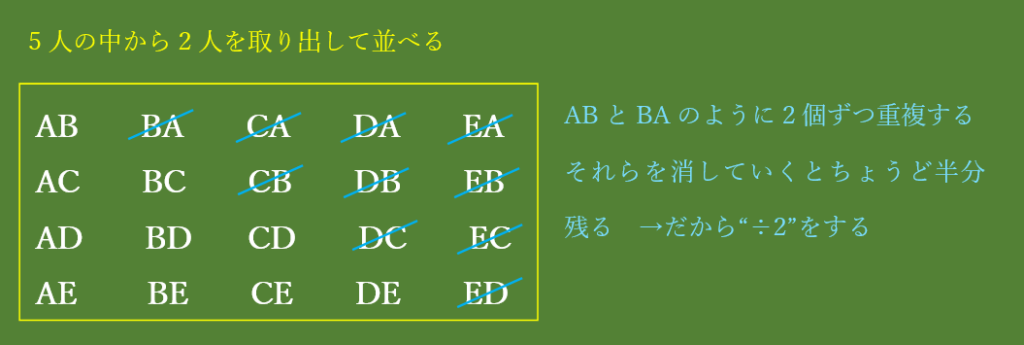

組み合わせを求めるときの”÷2”の意味が分かりました!組み合わせで考えたとき、2個ずつ重複があるので、
「”並べ方”の場合の数÷2」となるんですね!

並べ方は、5×4=20通り。
組み合わせは、20÷2=10通りになるんだ。
5人の中から3人を選ぶ計算

じゃあ、次は3人を選ぶ組み合わせのとき、何で割るんだったか覚えてるかな?

÷3でしたっけ?、÷6でしたっけ?

きちんと仕組みから理解しておこう!
では、例題を見てみよう!


さっきと同じ流れで、まずは、組み合わせを考える前に、5人の中から3人を選んで”並べる”んだ。全部書き出すのは大変だから、一部だけ書き出したぞ。
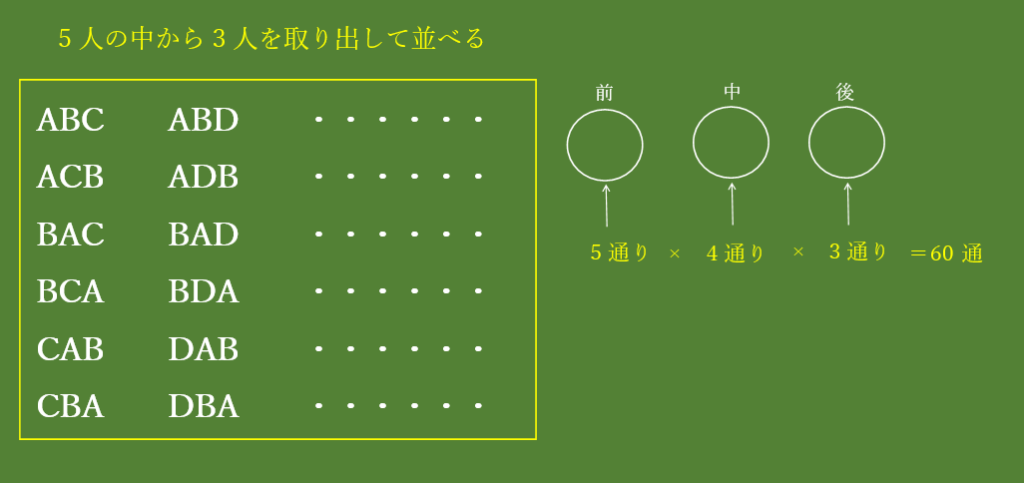

5人の中から3人を取り出して並べるのは、60通りもあるんですね!
まずは並べ方がわかったら、その次は、”いくつ重複があるか”、ですよね?

そう!さっきは、重複が2個ずつあったから、”÷2”をしたんだ。
じゃあ、今回は重複が何個あるのかな?図をよく見てみよう!

図の一番左の列は、よく見ると全部同じ組み合わせですね!並べ方は違うけど。
ということは、”÷6”ですね!
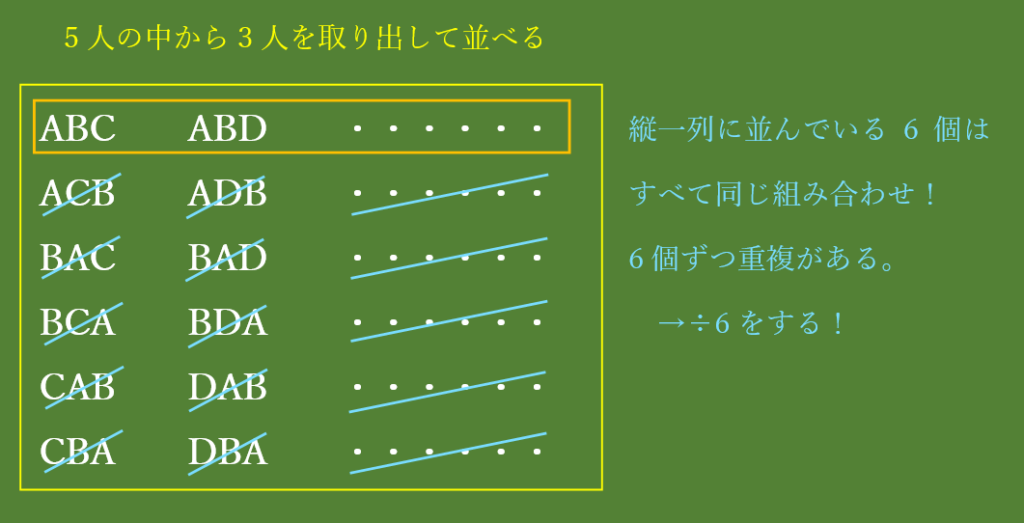

3人を選ぶ組み合わせを求めるときの”÷6”の意味が分かりました!組み合わせで考えたとき、6個ずつ重複があるので、
「”並べ方”の場合の数÷6」となるんですね!
3人だからといって、”÷3”ではないんですね!

並べ方は、5×4×3=60通り。
組み合わせは、60÷6=10通りになるんだ。

そういえば、さっきの2人の日直を選ぶ組み合わせも10通りだったような気がしますが、同じ答えになりましたね。偶然ですか?

いや、偶然じゃないんだ。
5人の中から3人を選ぶということは、2人を残すということだね。
つまり、[5人の中から3人を選ぶ組み合わせ]=[5人の中から2人を残す組み合わせ]ということがいえるんだ!

へ~、なるほど~!
まとめ
場合の数(組み合わせ)は、並べるところから考えると式の意味が理解できました。
お子様に解説する際にも、まずは並べ方を書き出してあげてください。
”÷2”、”÷6”の意味が納得できれば、場合の数も少しずつおもしろくなってくるはずです!


