”約数とは?”の基本から、入試に頻出の”約数を利用した文章題”まで理解しましょう!
また、約数に慣れておくと、”約分忘れ”も少なくなりますよ!
約数とは?

太郎くん、いきなりだけど、”約数”って何かな?

えっ!突然、聞かれると、、、えー、わり算できる数みたいな。。。

そうそう!そんな感じ!
約数とは、”ある整数を割り切ることができる整数”のことだ。
じゃあ、一つ聞いてみていいかな?6の約数は?

6の約数ですから、6を割り切ることができる整数のことなので、、、6÷1=6、6÷2=3、6÷3=2、6÷6=1と、1,2,3,6で割ることができました!

その通り!6の約数は、1,2,3,6の4個ということになるんだ!
6本のえんぴつを何人かの子供に分けるというとき、1人とか2人とか3人とか6人だったら、あまりなく分けることができるっていうことだ。
今、太郎くんがやってくれた、わり算の式4つで何か気づくことあるかな?

この式で気づくことですか? 6÷1=6、6÷2=3、6÷3=2、6÷6=1
えーと、あっ!わり算の答え(青)にも約数が全部出てきます!

そう!いいところに気が付いたね!
{6÷1=6、6÷2=3、6÷3=2、6÷6=1}
この4つの式って、6=1×6、6=2×3、6=3×2、6=6×1というように表すこともできるね。
わり算の答えも約数になるっていうこと!

約数を書き出していくときは、かけ算の形のペアで書き出していくといいです。
約数を書き出そう

じゃあ、太郎くん、12の約数を全部書き出してみてくれるかな?

はい、12をかけ算の形で書き出していきます。
12=1×12、2×6、3×4、、、で終わりですよね。
ということは、1と12、2と6、3と4の6個の数字になりました。

大正解!太郎くん、すごい!
じゃあ、次は16の約数を全部書き出してくれるかな?

はい、16をかけ算の形で書き出していきます。
16=1×16、2×8、4×4、、、で終わりだと思うんですけど、4が二つ出てきて、
ということは、1と16、2と8、4と4、、、で、6個?、いや、5個ですか?

4と4は、同じ数だから、正解は5個だね。1、2、4、8、16の5個だ!
約数が何個あるのか書き出していくと大体の数は、”偶数個”になることが多い。それは、○×△というように約数はペアで出てくるからなんだけど、16のように約数の個数が”奇数個”になるものもあるよ。
約数の個数が”奇数個”になるのは、4×4のようにペアが自分自身と同じ数字になる数です。このように同じ数字の積になっている数を”平方数(四角数)”といいます。”平方数(四角数)”は、約数の個数が奇数個になります。
公約数・最大公約数

太郎くん、今度は18の約数と24の約数を、それぞれ書き出してみてくれるかな?

はい、
18=1×18,2×9,3×6ですから、18の約数は{1,2,3,6,9,18}
24=1×24、2×12、3×8、4×6ですから、24の約数は{1,2,3,4,6,8,12,24}
になりました。

そうすると、両方に共通する約数があるんだけど、どれかな?

はい、
18の約数{1,2,3,6,9,18}、24の約数{1,2,3,4,6,8,12,24}に共通するのは、{1,2,3,6}の4つです。・・・これが何なんでしょうか?

約数を書き出すのが上手になったね!
それで、18と24に共通する約数{1,2,3,6}を取り出してもらったんだけれど、これらの数を、18と24の公約数っていうんだ。この中でも最も大きい公約数を、最大公約数っていうんだけど、入試頻出の文章題で使うから、絶対覚えておこう!

じゃあ、18と24の最大公約数は6で、公約数は1,2,3,6ということですよね?!
先生、そうすると、公約数1,2,3,6は、最大公約数6の約数になってませんか?!

おー!よく気が付いた!その通り!
18も24も、両方とも6で割れるんだから、当然、1でも2でも3でも割れるでしょっていう話だ!
ある二つの整数の公約数は、最大公約数の約数になっている。
上の例でいえば、18と24の公約数{1,2,3,6}は、18と24の最大公約数6の約数になる。
最大公約数の求め方

じゃあ、先生、最大公約数を求めることができれば、公約数はわかるっていうことですよね!?
それぞれ約数を全部書き出さなくてもいいってことですよね!?

その通り!
18と24の公約数を知りたければ、最大公約数6を求めてあげることで、あとは6の約数をかきだしてあげればいいんだ!
最大公約数の求め方には、”連除法”という便利な方法があります。2ステップです。
①18と24を共通して割れる数で割っていきます。右の例では、まずは2で割って、その次に3で割りました。
②次に、それらの数をかけ合わせたら終了です。2×3=6が最大公約数です。


へ~、じゃあ、公約数をもとめるとき、それぞれの約数をいちいち全部書き出さなくても、
①まず最大公約数求めて、②その約数を求める、という2段階でやればいいんですね!
約数を利用した文章題(入試に頻出)

だいぶ約数について、理解が深まってきたと思うよ!
それじゃあ、入試によく出てくる文章題を一つやってみようか!


赤玉30個は全部配ることができたので、子どもの人数は30を割ることができる数、つまり、30の約数ですよね?!

その通り!バッチリ!

それで、次に青玉は何個配ることができたのかというと、48ー3=45個だから、子どもの人数は45を割ることができる数、つまり45の約数で間違いないですか!

見事!バッチリ!

ということは、両方合わせて考えると、子どもの人数は30の約数であり、45の約数でもあるので、つまりは30と45の公約数ということですね!

ハイ!いいね!
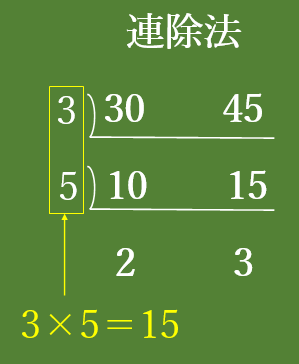

じゃあ、さっきの手順で30と45の最大公約数を求めてみます。
連除法を使って、3×5=15になりました。
・・で、次は何をするんだったっけ・・・
そうだ!①最大公約数→②公約数の流れでした!
15=1×15,3×5 だから、小さい順に、1,3,5,15だ。
ということは、子どもの人数は1人、3人、5人、15人でいいのかな・・・?

青玉は全部で48個あって、3個あまったとあるから、子どもの人数が1人だったら、そもそも3個あまらないなあ。
子どもの人数が3人だったとしたら、あまった3個を3人にそれぞれ1個ずつ配って、やっぱりあまらないなあ。

わかりました!青玉のあまりが3個あるから、子どもの人数は3人より多くないといけないんですね!ということは、考えられる子どもの人数は5人と15人です!

バッチリ!大正解!!
約数を利用した入試頻出の文章題でしたが、公約数1,3,5,15を全部答えにしてしまうミスが多いです!青玉のあまり3個より多い人数を答えるということに注意!!
まとめ
”数の性質”の分野の最も基本的な単元、”約数”について説明いたしました。
この基本が理解できていれば、たいていの問題に応用可能です!
まずは、きちんと理解したうえで演習量をこなしましょう!


