”倍数とは?”の基本から、倍数を利用した頻出問題までマスターしてしまいましょう!
また、倍数に慣れておくと、分数の計算にもとても強くなりますよ!
倍数とは?

太郎くん、いきなりだけど、”倍数”って何かな?

えっ!突然、聞かれると、、、えー、2倍、3倍、4倍・・・してできる数みたいな。。。

そうそう!まさにそんな感じ!
倍数とは、”ある整数を1倍、2倍、3倍、・・・してできる整数”のことだ。
じゃあ、一つ聞いてみていいかな?6の倍数を小さい順に3つ教えてくれるかな?

6の倍数ですから、6×1=6、6×2=12、6×3=18です。6の段ですね。

その通り!倍数というのは、1倍、2倍、3倍、・・・と無限に作ることができるよ!
だから、6×1000=6000 これも6の倍数だ。
公倍数・最小公倍数

太郎くん、今度は4の倍数と6の倍数を、数直線上に示してくれるかな?

はい、こんな感じになりました。
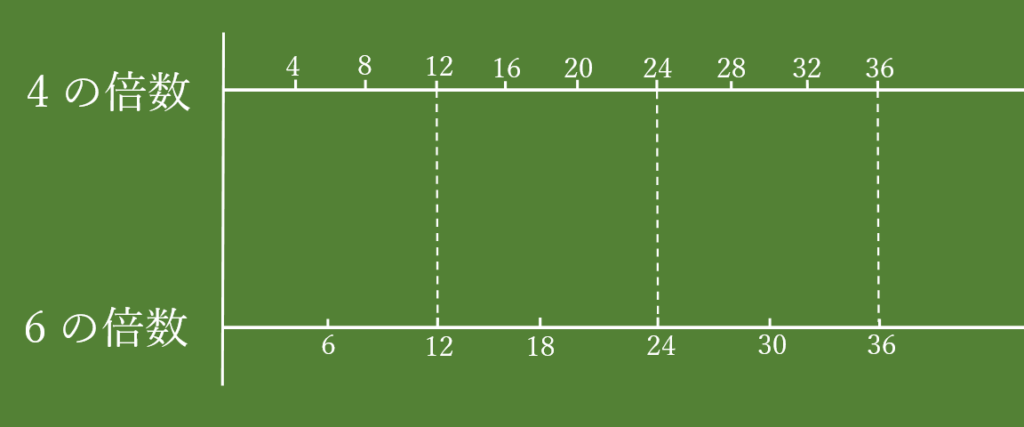

おー!きれいに書けたね!そうすると、両方に共通する倍数があるね、12、24、36とか。これらの数を、4と6の公倍数っていうんだ。12ごとに現れるから、次は48、60、72・・・と続いていく。そして、最も小さい公倍数を、最小公倍数っていうんだけど、これは分数の足し算・引き算でよく使うから、計算得意になるためにも覚えておこう!

先生、4と6の最小公倍数は12で、公倍数は12,24,36,48、60、72・・・ということですよね?!
そうすると、公倍数12,24,36,48,60、72・・・は、最小公倍数12の倍数になってますね!?

おー!よく気が付いた!その通り!
12が、4と6の公倍数なんだから、12の倍数もまた、当然、4と6の公倍数になってるでしょっていう話だ!
ある二つの整数の公倍数は、最小公倍数の倍数になっている。
上の例でいえば、4と6の公倍数12,24,36,48、60、72・・・は、4と6の最小公倍数12の倍数になる。
最小公倍数の求め方

じゃあ、先生、最小公倍数を求めることができれば、公倍数はわかるっていうことですよね!?
それぞれ倍数を全部書き出さなくてもいいってことですよね!?

その通り!
4と6の公倍数を知りたければ、最小公倍数12を求めてあげることで、あとは12の倍数を書きだしてあげればいいんだ!
約数のところで連除法を学んだけれど、それは最小公倍数を求めるときにも使えるんだ!
最小公倍数の求め方にも、”連除法”が使えます。最大公約数のと同じく2ステップです。
右の例では、18と24の最小公倍数を求めます。
①18と24を共通して割れる数で割っていきます。右の例では、まずは2で割って、その次に3で割りました。
②次に、外側の数をすべてかけ合わせたら終了です。2×3×3×4=72が18と24の最小公倍数です。

倍数を利用した頻出問題

だいぶ倍数について、理解が深まってきたと思うよ!
それじゃあ、ちょっと難しいけど、入試問題を一つやってみようか!

わかりました!頑張ってみます!


なんか、全体的に数字が大きいですね・・・4桁とか出てくるし・・・
うーん、まず28で割って5余る数を書き出してみるかな、28×1+5=33、28×2+5=61、28×3+5=89,28×4+5=117・・・5も含めると、5,33,61,89,117・・・こんな感じだな。。。

すごくいいね!書き出してくれた数、どんな数かな?もちろん、28で割って5あまる数なんだけど、倍数という言葉を使って表せるかな?

あー、自分の式を見て気づいたんですが、28の倍数に5を加えてます!
じゃあ、63で割って5余る数というのも、63の倍数に5を加えた数ということですね!

おー!バッチリだよ!
じゃあ、28で割っても5余り、63で割っても5余る数というのは、どんな数かな?

はい、えー、、、
28と63の公倍数に5を加えた数ということですね!

おー!バッチリ!
その公倍数で4桁の最も小さい数を探さないといけないね!

はい、ひとまず28と63の最小公倍数を求めてみます!
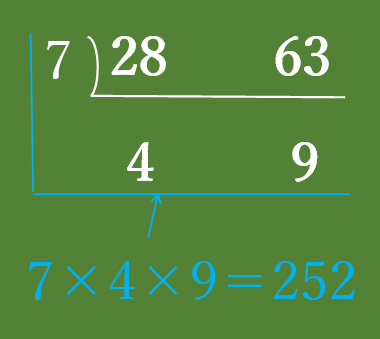

連除法で最小公倍数が252になりました。ここまで合ってますでしょうか?

合ってるよ!次は、28と63の公倍数で4桁の最も小さい数を求めよう!

28と63の公倍数は、252から始まって、252×2、252×3、252×4で4桁になりますね!
252×4=1008 4番目に小さい公倍数で4桁になりました。
最後はこれに5を足して、1008+5=1013です!

おー!バッチリ!大正解だ!!
すごいね、太郎くん!倍数に対する理解がいっそう深まったと思うよ!
まとめ
”数の性質”の分野の最も基本的な単元、”倍数”について説明いたしました。
倍数が得意になると、計算も速く・正確になります!
しっかり基本を理解して、ステップアップしていきましょう!


